Die Ableitung einer Funktion gibt die Steigung in jedem Punkt an, d.h. ob die Werte in einem bestimmten Punkt größer oder kleiner werden, und um welchen Betrag sie sich ändern.

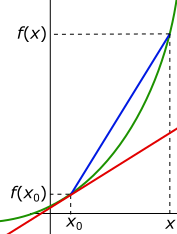
Im Bild rechts ist ein Funktionsgraph eingezeichnet. Die Steigung am Punkt P(x0|f(x₀)) ist durch die Tangente gekennzeichnet. Die Gerade durch die Punkte P(x₀|f(x₀)) und Q(x|f(x)) (Sektante) ist eine Näherung für die Tangente. Die Steigung einer Geraden kann mit dem Steigungsdreieck berechnet werden.

Damit sich die Sekante der Tangente annähert, muss der Abstand zwischen x und x₀ verkleinert werden, d.h. x muss gegen x0 laufen. Dies wird im Differenzenquotienten durch den Limes ausgedrückt:

f'\left(x_0\right)=\lim_{x\longrightarrow x_0}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}

Beispielrechnung für f\left(x\right)=\frac{1}{x}:

f'\left(x\right)=\lim_{x\longrightarrow x_0}\frac{\frac{1}{x}-\frac{1}{x_0}}{x-x_0}=\lim_{x\longrightarrow x_0}\frac{\frac{x_0}{x\cdot x_0}-\frac{x}{x\cdot x_0}}{x-x_0}=\lim_{x\longrightarrow x_0}\frac{\frac{x_0-x}{x\cdot x_0}}{x-x_0}

=\lim_{x\longrightarrow x_0}\frac{x_0-x}{x\cdot x_0}\cdot\frac{1}{x-x_0}=\lim_{x\longrightarrow x_0}\frac{x_0-x}{x\cdot x_0}\cdot\frac{1}{-1\left(x_0-x\right)}=-\frac{1}{x^2}