Extremstellen einer Funktion bestimmen
Extremstellen sind die x-Werte, an denen unsere Funktion einen Hochpunkt (Maximum) oder einen Tiefpunkt (Minimum) besitzt.
Den dazugehörigen y-Wert bezeichnet man als Extremwert.
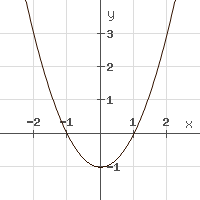
1. Unsere Funktion
f\left(x\right)=x^2-1
2. Berechnen der ersten Ableitung
f'\left(x\right)=2x
3. Davon die Nullstellen bestimmen
0=2x hat nur die Lösung x_0=0
4. Berechnen der zweiten Ableitung
f''\left(x\right)=2
5. Einsetzen der Nullstellen aus Schritt 3
f''\left(0\right)=2
6. Schlussfolgern aus den Berechnungen
- lokales Minimum: wenn f'\left(x_0\right)=0 und f''\left(x_0\right)>0
- lokales Maximum: wenn f'\left(x_0\right)=0 und f''\left(x_0\right)<0
In unserem Beispiel haben wir ein Minimum an der Stelle x_0=0. Notwendig hierfür war, dass die Steigung an diesem Punkt 0 ist (3) und die zweite Ableitung an diesem Punkt > 0 ist (5).

Kommentare